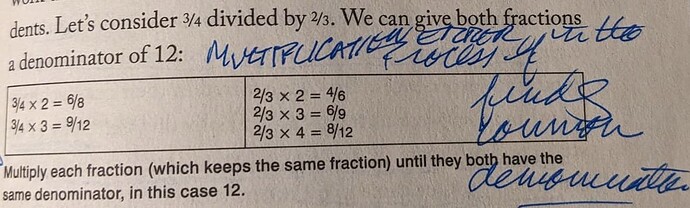I happened to come across a tweet about a new book by Jo Boaler, Math-ish. The author of the tweet, Ling Huang (AKA @FightFuzzyMath) showed a screenshot of page 165 of her copy with handwritten notes. In particular, this table:
The first problem, of course, is that \dfrac{3}{4} \times 2 = \dfrac{6}{4}, not \dfrac{6}{8} and so on. What was likely meant was \dfrac{3}{4} \times \dfrac{2}{2} = \dfrac{6}{4}, which works because \dfrac{2}{2} = 1 and multiplying any number by 1 equals itself.
Many of the replies to the tweet suggested that this was probably a typo not caught be the editors. That’s likely true, but not much comfort. Math errors in a book about math cast doubt on the entire book. How many other errors have crept into the text?
I also pointed out:
[You] don’t need like denominators for dividing by a fraction! Just multiply by the reciprocal. Having the same denominator is handy for addition and subtraction.
I got several replies around the idea that students should get a variety techniques and not just apply an algorithm to get to the answer quickly. As it happens, I agree. I distinctly remember my 6th grade teacher, Mr King, telling us that many adults fail to understand fractions and just apply the formulas. He showed us an example from his tax calculations and explained how really understanding fractions helped him solve the problem.
As the blurb about the book explains:
In Math-Ish, Boaler shares new neuroscientific research on how embracing the concept of “math-ish”—a theory of mathematics as it exists in the real world—changes the way we think about mathematics, data, and ourselves. When we can see the value of diversity among people and multi-faceted approaches to learning math, we are free to truly flourish.
So I asked my twins, who are just starting 6th grade, how they learned to do division of fractions. My son immediately went to finding a common denominator. My daughter didn’t remember so she said she’d start with a diagram. I asked them if they had learned about inverting fractions and my daughter had. She said she’d do it that way since it’s faster than finding common denominators.
I gave my son a sample problem because he loves doing math problems in his head:
He thought about it and said 2 \frac{1}{2}. Then, after a beat, he said “in sixths”. No doubt he’s thinking about converting fractions into the same denominator a bit like converting to the same unit of measure to make calculations easier. That simplifies the math problem because you can cancel the sixes:
But what happened to the units? He hasn’t learned dimensional analysis just yet so its understandable he doesn’t know that like units cancel when divided, just as like numbers cancel.
Which brings me back to Mr. King. He taught me the key to unlocking fractions.
The one thing you need to understand fractions is that they are just another way to write division. Not analogous or similar to division, but identical to division. The following expressions mean exactly the same thing:
And even:
What this means is that you can abstract away the details. “Flipping and multiplying” isn’t a quick algorithm for solving division by fraction problems, but an essential tool for manipulating symbols. The symbols could represent anything: numbers, variables, units, recipe ingredients, chemical elements, distances on maps, etc. If you understand that multiplying by the reciprocal is identical to division, you have a new method to solve all sorts of problems.
Very soon my twins will be learning algebra. to be successful, they must learn that math isn’t a way to solve problems about numbers but rather a system of symbol manipulation that can be applied to arithmetic. Techniques like finding common denominators and multiplying by the inverse fraction will serve you long after you finish your last math class in school.
The page from Math-ish included this sentence:
For division of a fraction by a fraction (something most people have never used in their lives after school), I prefer to make both fractions have the same denominator first.
We’ve been doing construction at our house and when I come to look over the work, I’ve found cryptic notes on the framing that will later be covered with drywall.
This particular note indicates the length of a support beam. The guys doing the tiling left calculations for how many 4 \times 11 \frac{3}{4} inch tiles fit on the wall. For anyone in the building trades, division by fractions is a regular part of the job. From the notes they left, our workers seem to do the math in their heads. I wonder if they divide by finding a common denominator or inverting fractions or some other technique I haven’t learned yet.
Math is power… especially in construction.